Can we simulate complex multidimensional multiphysics problems efficiently on quantum computers?
To address this problem properly we have to dig a little bit deeper into not only the multiphysics problem that we are trying to simulate but into the mathematical model that can be efficiently implemented on quantum computers also.
Luckily, the quantum lattice Boltzmann method (LBM) offers a solution, again.
Understanding dimensionality in multiphysics simulations
When we want to simulate some physical processes in practice, the need for details in the results often imposes the dimensionality of the mathematical model being used. The less information we need, the simpler the model we can use.
To mathematically describe the same physical process operating on different dimensional levels, certain modifications (simplifications) of the basic equations need to be introduced.
One-dimensional models where only one spatial coordinate is being considered include the highest level of simplification, while the two (2D) and three-dimensional (3D) models are far more complex.
In the case of two and three-dimensional models, geometry describing the boundaries of the physical domain is more involved, therefore requiring more computational power. Here the quantum jumps into the game.
Expanding the QLBM for multidimensional challenges
The Quantum lattice Boltzmann method (QLBM), Quanscient’s flagship procedure for solving computational fluid dynamics problems on quantum computers, can be further extended to simulate higher dimensional Multiphysics problems.
Each computational step of the QLBM described previously for the 1D case can be efficiently simulated on quantum devices for 2D and 3D cases.
In contrast to the 1D case, where we can have two or three distribution probabilities per lattice site, in a higher dimension domain, more distribution probabilities per node are required. In the 2D LBM, for example, we can have five or nine probabilities per node, depending on the configuration of the model.
As a consequence of having more distribution functions per lattice site, the propagation step now involves evolution in four (nine) spatial directions, while the collision step can include more additional terms in the equilibrium distribution function (complex dynamics require more information).
From the quantum computing perspective, implementation of these steps can be performed efficiently in a similar manner as in the 1D case with some additional modification in order to include additional degrees of freedom.
Applying the Quantum D2Q5 model in 2D simulations
To demonstrate the application of the two-dimensional quantum lattice Boltzmann method transport of constituents governed by the advection-diffusion equation (ADE) is simulated using the Qiskit, IBM’s SDK for working with quantum computers.
Time evolution of the concentration drops Cmax=1.0 at the position x=20 and y=20 of the rectangular domain carried by the flow velocity components ux=0.1 and uy=0.1 after t=100 time steps are shown in Figure 1 (red line corresponds to analytical solution).
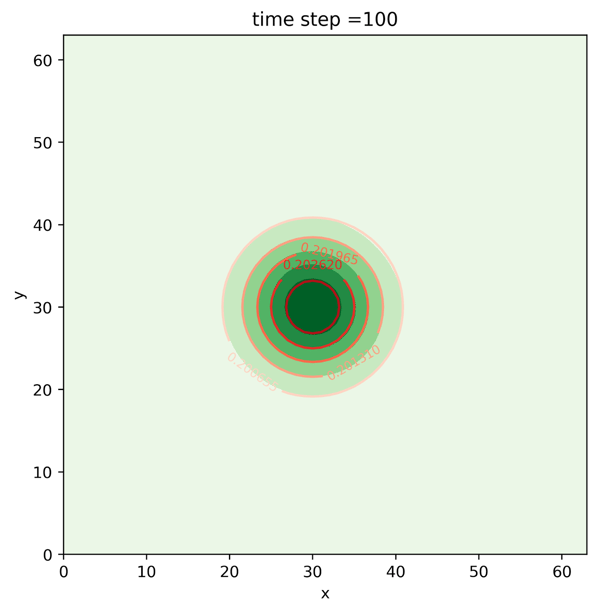
Concentration profile after 100-time steps calculated with the 2D QLBM
Conclusion
- Simulation of the physical process in higher dimensions is more complex in contrast to simplified 1D cases.
- The lattice Boltzmann method can easily simulate processes in higher dimensions while maintaining its simplicity at the same time.
- LBM for higher dimension cases involves lattice models with additional propagation directions (in contrast to the 1D case) followed by the implementation of some additional terms in the equilibrium distribution function.
- Quantum implementation of the higher dimension LBM models utilizes the same methodology used in 1D QLBM. However, due to the additional directions in the lattice structure development of the corresponding quantum algorithm is now more involved.
- The quantum lattice Boltzmann method shows significant potential for performing multidimensional multiphysics simulations on quantum computers.
