How we are accelerating superconductivity simulations with the H-𝝓 formulation

Advancements in the field of applied superconductivity hinge upon precise and efficient simulations.

However, these often encounter roadblocks, such as computational demands and numerical instability.

Our cloud-based multiphysics simulation platform, Quanscient Allsolve, addresses these challenges with the H-𝝓 formulation, a robust mathematical framework developed for magnetoquasistatic simulations.

By enhancing numerical stability, accuracy, and significantly reducing computation time, this 
approach provides a practical and efficient solution for superconductivity simulations.

In this article, we explain the benefits of the H-𝝓 formulation as opposed to the conventional H-formulation, and show how Quanscient Allsolve effectively employs it.

The problem with the conventional H-formulation

The conventional H-formulation serves as the backbone of numerous simulations in applied superconductivity.

By solving Faraday's law in terms of the magnetic field strength H, this technique effectively captures the dynamics of the magnetic field within a modeling domain.

Yet, for all its utility, the H-formulation encounters significant pitfalls when applied to non-conducting domains. To avoid the manifestation of eddy currents within these non-conducting regions, very high dummy resistivity is typically assigned.

However, this approach can lead to an ill-conditioned system matrix, which poses a substantial risk of numerical instability. In AC simulations, where alternating external magnetic field and current are present, these circumstances might cause unphysical current leaks in the air domain - a significant challenge, particularly when determining the AC loss of superconductors.

Moreover, the H-formulation incurs an unnecessarily large number of Degrees of Freedom (DOFs). These additional DOFs plus  the ill-conditioning of the system matrix results in elevated computation times.

In the realm of superconductors, especially when simulating large systems such as electrical machines and fusion devices, these limitations quickly reach their breaking point. The H-formulation, although robust in many applications, struggles to efficiently handle the complexity and scale of these simulations, leading us to seek a more advanced and efficient approach: the H-𝝓 formulation.

H-𝝓 formulation in superconductivity simulations

The novel H-𝝓 formulation, as employed in Quanscient Allsolve, is a leap forward in the realm of superconductivity simulations.

This formulation effectively marries the benefits of the well-known H-formulation with the 𝝓-formulation, which utilizes the magnetic scalar potential in non-conducting regimes. The result? A transformation in the way we approach superconductor simulations.

Unlike the H-formulation, the H-𝝓 formulation splits the computational domain into two distinct regimes: conducting and non-conducting. Within the non-conducting regime, the magnetic scalar potential 𝝓 (H = - grad 𝝓) is used. This nuanced approach has profound implications for the efficiency and stability of simulations.

Firstly, dealing with scalar unknowns in non-conducting regimes, as opposed to vectorial unknowns, drastically reduces the DOFs. Fewer DOFs translate to lower computational overhead, effectively speeding up computation times. This is particularly beneficial when working with large systems such as electrical machines and fusion devices.

Secondly, the term containing the electric resistivity, which can lead to an ill-conditioned system in the H-formulation, naturally vanishes in non-conducting domains in the H-𝝓 formulation. This elimination enhances the stability of the system, avoiding unphysical phenomena and improving the overall reliability of simulations.

By incorporating the H-𝝓 formulation, Quanscient Allsolve achieves more stable, faster, and physically accurate solutions. But how exactly does this formulation work? 

How Quanscient Allsolve harnesses the H-𝝓 formulation

First, let's revisit the division of the computational domain into conducting and non-conducting regions. This is a crucial part of the H-𝝓 approach and has a direct impact on how different elements are treated.

In conducting regions, we use edge elements in the first order of interpolation and adhere to the usual H-formulation. This traditional approach offers reliable performance in these areas where conductivity plays a significant role.

On the other hand, in non-conducting regions, we use Lagrangian elements with nodal DOFs. Here, the magnetic field is written in terms of a magnetic scalar potential, such that H = -grad 𝝓.

By applying this formulation, we effectively force the current density J to be zero in non-conducting regions, following the principle that J = curl H = curl (- grad 𝝓) = 0. In these domains, the term containing the electric resistivity naturally vanishes, leading to a stable and well-conditioned system.

However, the 𝝓-physics does introduce a specific challenge. Ampere’s law dictates that every closed loop integral over H must result in 0, which is confirmed as J = curl H = curl (- grad 𝝓) = 0. But if the loop surrounds the conducting domain, it should equal the net current in our case. This is contradictory to the definition of 𝝓.

We address this issue by introducing cohomology cuts. This technique ensures that the circulation of the magnetic field around conducting domains matches the desired net currents. Essentially, we impose a discontinuity of 𝝓 on a line (or surface) in 2D (3D) connecting the air domains to the conductor.

This discontinuity makes any loop in the 𝝓-physics obey Ampere's law, giving every loop integral of the magnetic field surrounding a conducting domain a jump equal to the enclosed current.

This thoughtful application of the H-𝝓 formulation in Quanscient Allsolve enhances computational performance, stability, and the accuracy of superconductor simulations, making it an invaluable tool for professionals in the field. As we look forward, Quanscient Allsolve is poised to continually revolutionize what's achievable in the world of superconductivity simulations.

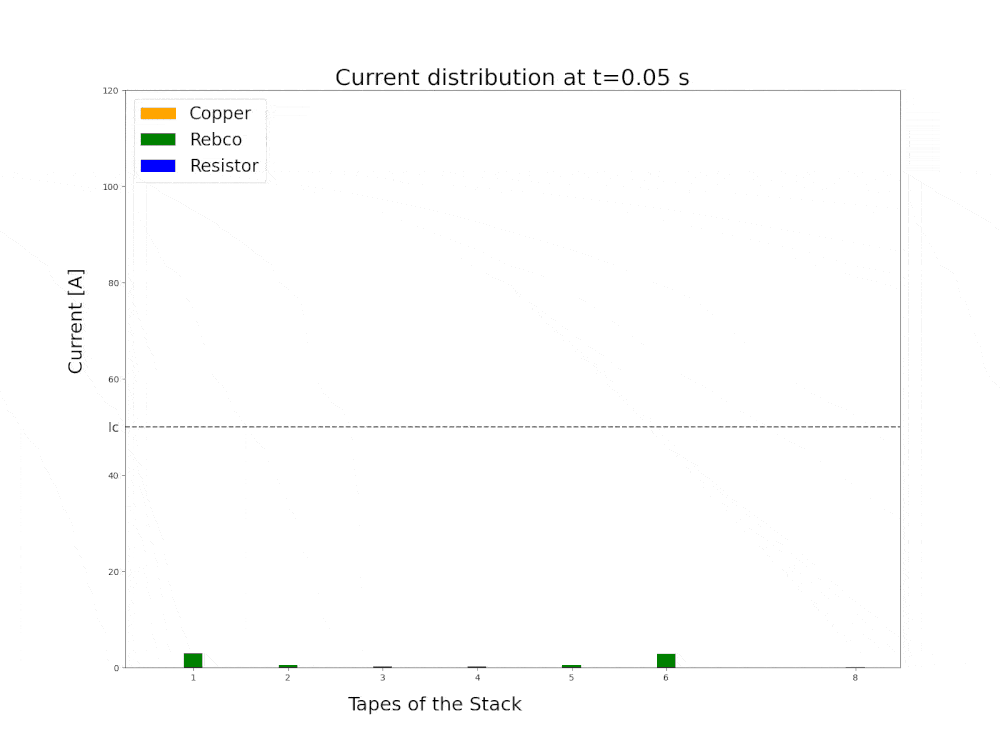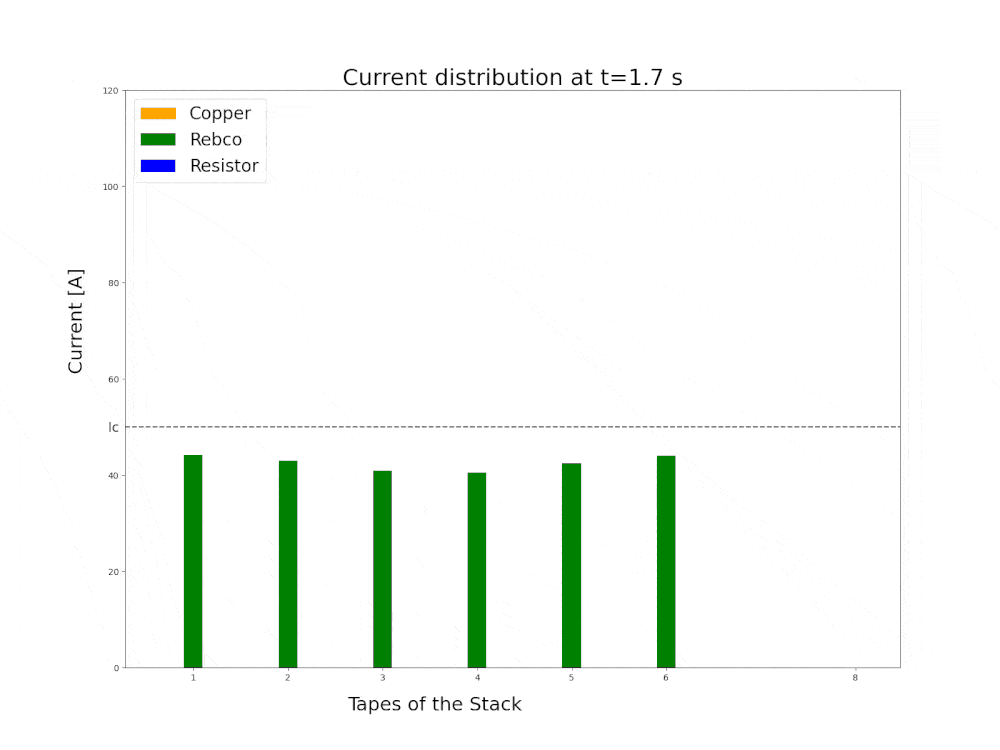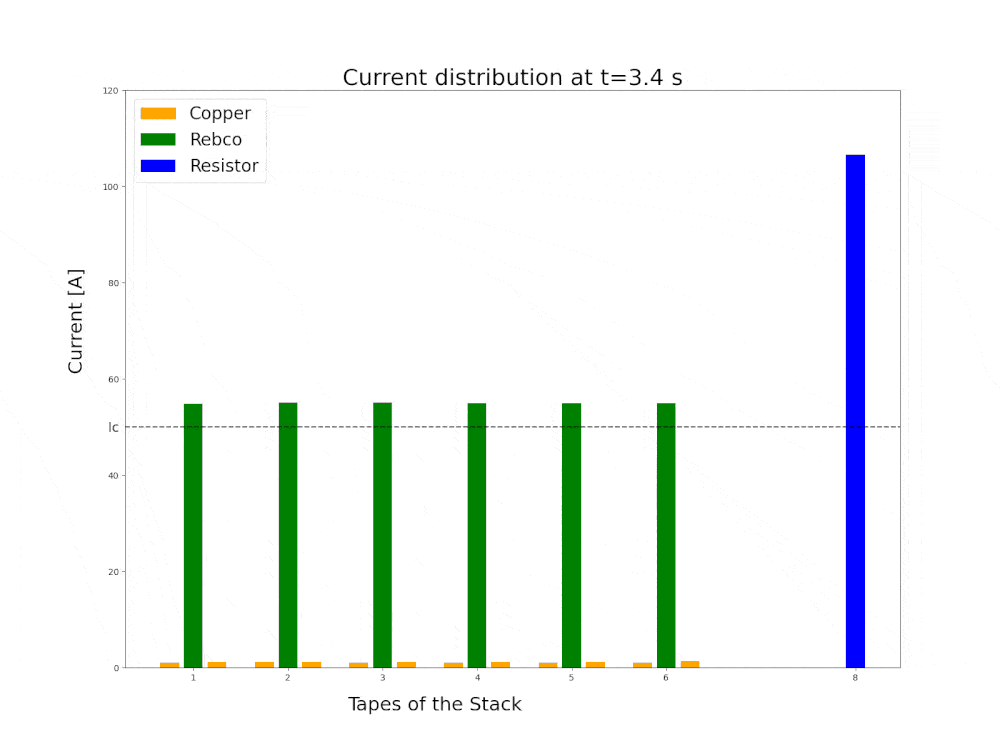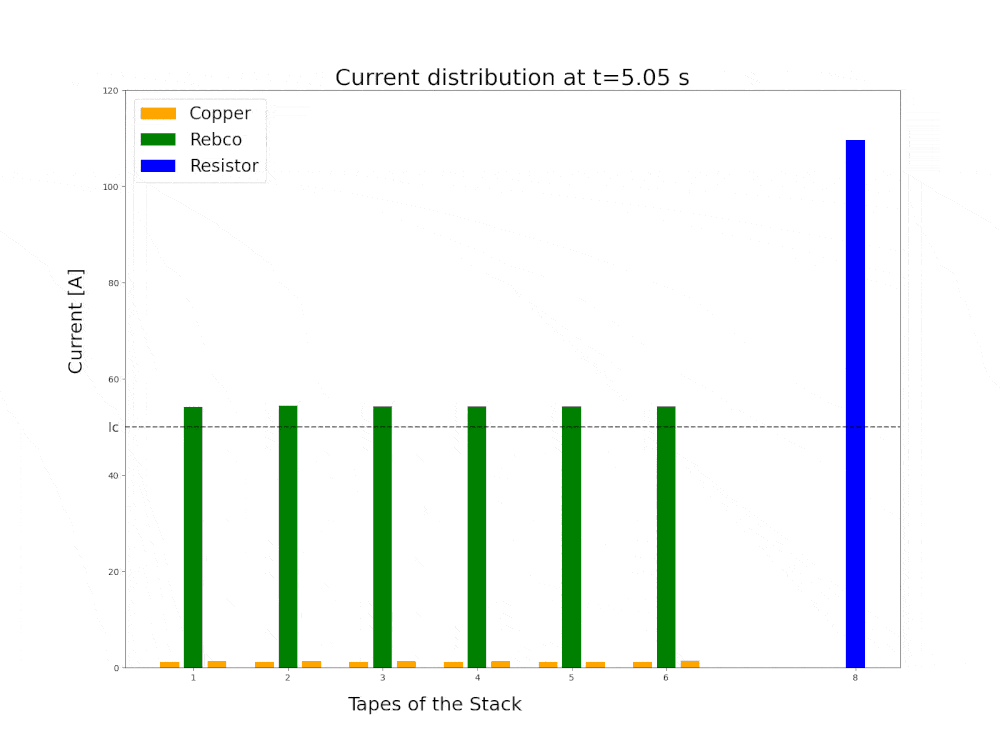
Superconductor quench full 3D FEM simulation using h-phi formulation
Current redistribution in a stack of 6 YBCO tapes with parallel quench protection lumped resistance.

Conclusion

In the intricate world of superconductivity simulations, precision, efficiency, and accuracy are paramount. Standard H-formulation, while reliable, exhibits limitations, especially in the context of large-scale models including non-conducting domains.

It is against this backdrop that the H-𝝓 formulation and Quanscient Allsolve enter the scene, ready to redefine the simulation landscape.

Providing the H-𝝓 formulation for 3D magnetics FEM fully automatic in the GUI we enable simulations with fewer DOFs, more stable systems, and faster, physically accurate solutions.

So, whether you're designing an electrical machine or working on a fusion device, the robustness, speed, and accuracy brought by Quanscient Allsolve and the H-𝝓 formulation can be your competitive edge.

As we continue to advance our platform, we invite you to explore the possibilities of superconductivity simulations with us.

Together, we can continue to extend the capabilities of superconductivity simulations, contributing to a future that takes full advantage of the extensive potential of superconducting materials.

Read more about our capabilities and book a demo on our superconductor page.

Summary

• The H-𝝓 formulation, employed by Quanscient Allsolve, enhances computational stability and accuracy while reducing computation time for superconductivity simulations.
• The conventional H-formulation, despite its robustness, can lead to numerical instabilities, elevated computation times, and potential unphysical phenomena when applied to non-conducting domains.
• The H-𝝓 formulation combines the H-formulation with the 𝝓-formulation, using the magnetic scalar potential in non-conducting domains, effectively reducing degrees of freedom and system instability.
• In Quanscient Allsolve's implementation of the H-𝝓 formulation, the computational domain is split into conducting and non-conducting regions, with different strategies employed for each, leading to a more accurate and stable solution.
• The H-𝝓 formulation introduces a challenge with respect to Ampere’s law, which is addressed in Quanscient Allsolve through the use of cohomology cuts, ensuring an accurate representation of net currents in the conducting domains.
• To the best of our knowledge, Quanscient Allsolve is the first and only commercial software providing general, fully automatic h-𝝓 3D magnetics FEM simulations trivially in the GUI.