Is it possible to reproduce multiple physical processes using quantum computers?
Moreover, is it possible to do this more efficiently than by using classical computers?
The classical approach
To simulate, for example, a moving fluid on a classical computer, a common methodology includes the transformation of the corresponding partial differential equations (PDE) describing the system into a set of algebraic equations and then using a computer to solve it.
This transformation involves transferring the PDEs into their discrete counterparts over some temporal-spatial domain covered with the computational grid using numerical techniques like the finite difference method (FDM) or finite element method (FEM).
Finally, the dimensionality of the discretized system being solved and the required computational resources depend on how large and complex the physical system is.
The lattice Boltzmann method
The Lattice Boltzmann Method (LBM) is an alternative approach to the classical multiphysics solvers for fluid flow. Instead of solving, for example, the Navier-Stokes equations directly (FDM, FEM), a fluid density on a lattice is simulated with streaming and collision (relaxation) processes.
Fluid density is replaced with fictive particles described as the distribution functions fi, which undergoes a propagation and collision in the mesoscopic environment process over a discrete lattice (grid) covering the fluid domain.
The connection between macroscopic variables (velocity, pressure) and the mesoscopic domain, described by distribution functions, is achieved by simple (linear) summation of the discrete speeds.
Due to its particulate nature and local dynamics, LBM has several advantages over other conventional CFD methods, especially in dealing with complex boundaries, incorporating microscopic interactions, and algorithm parallelization.
The quantum lattice Boltzmann method
Why go quantum LBM? The main motivation behind utilizing the LBM for fluid flow simulations on quantum computers lies in the high degree of analogy between the systems (classical and quantum), making the LBM more “quantum native” than the standard numerical techniques.
The dynamical variables in both systems are based on some form of probability, allowing us to implement an explicit mapping between these two systems.
The time evolution of the probabilities in the LBM can be mapped to the discrete quantum system used in quantum computations so that the simulation process can be entirely performed on a quantum computer.
The quantum D1Q2 model
To demonstrate the application of the quantum lattice Boltzmann method (QLBM), one dimensional (1D) advection-diffusion equation (ADE) for transport of the concentration of some constituent is simulated using Qiskit.
For this purpose, an example of arbitrary constituent movement (pollution, sediment, etc.) along a straight channel with the flow velocity u=0.1, location of the drop xdrop=12, maximal concentration of Cm=1.0, and initial concentration Ci=0.5 is simulated.
The quantum lattice Boltzmann method shows significant potential for quantum-native multiphysics simulations using quantum computers.
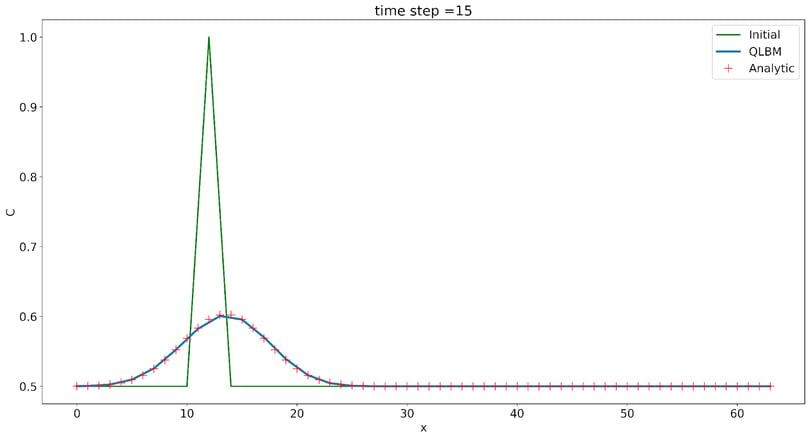
Concentration profile after 15 time steps calculated with the 1D QLBM.
Conclusion
- Simulating physical processes on classical computers involves transforming partial differential equations into algebraic equations and solving them using numerical methods like finite difference or finite element methods.
- The Lattice Boltzmann Method is an alternative approach to classical solvers for fluid flow that simulates evolution of fictitious particles on a lattice using streaming and collision processes.
- The Lattice Boltzmann Method has advantages over other conventional computational fluid dynamics methods, particularly in dealing with complex boundaries and incorporating microscopic interactions.
- The Lattice Boltzmann Method can be mapped to the discrete quantum system used in quantum computations, making it a promising approach for quantum-native multiphysics simulations.
- A one-dimensional advection-diffusion equation for the transport of a constituent along a straight channel was simulated using the quantum lattice Boltzmann method in Qiskit.
- The quantum lattice Boltzmann method shows significant potential for performing multiphysics simulations on quantum computers.